문제
M이상 N이하의 소수를 모두 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 자연수 M과 N이 빈 칸을 사이에 두고 주어진다. (1 ≤ M ≤ N ≤ 1,000,000) M이상 N이하의 소수가 하나 이상 있는 입력만 주어진다.
출력
한 줄에 하나씩, 증가하는 순서대로 소수를 출력한다.
접근
소수를 찾는 방법은 다양한데 에라토스테네스의 채를 이용해 보았습니다.
범위 내 각각의 수가 소수인지를 찾는 것보다 메모리 사용량은 증가하지만 M~N의 범위가 넓을 때엔 훨씬 효율적입니다.
범위가 1 ≤ M ≤ N ≤ 1,000,000이니 각각을 구하는 것도 시간 제한에 걸리지는 않았지만 에라토스테네스의 채를 이용하는 것이 적합해 보입니다.
[2581]소수 찾기 여기서 이용한 방식을 loop문으로 활용해도 시간 제한에 걸리지 않습니다.
에라토스테네스의 채
문제에 적용하기 위해 에라토스테네스의 채가 무엇인지 짚고 넘어가겠습니다.
2~N 까지의 수 중에서 소수를 가려내기 위해 채처럼 소수 외의 수를 걸러내는 것입니다.
걸러지지 않은 수 중 가장 작은 수를 배제하고 그 수의 배수를 걸러냅니다.
또 걸러지지 않고 남은 것들에서 위 수행을 반복합니다.
걸러내기 전에 확인할 것은 1은 소수가 아니기 때문에 걸러내는 범위는 2부터 시작합니다.
2부터 2의 배수를 걸러내고, 3의 배수를 걸러내고… 이런 식으로 걸러냅니다.
자동적으로 소수는 걸러지지 않고 남게 됩니다.
참고해서 아래 gif 파일을 확인해 주세요.
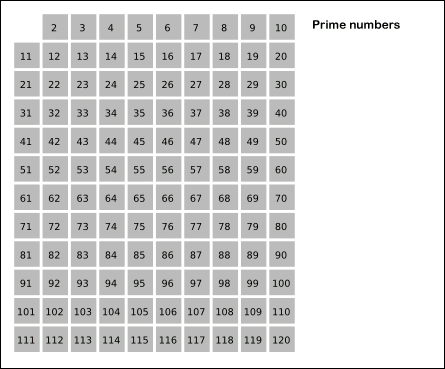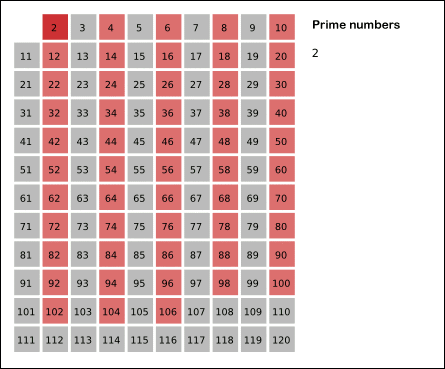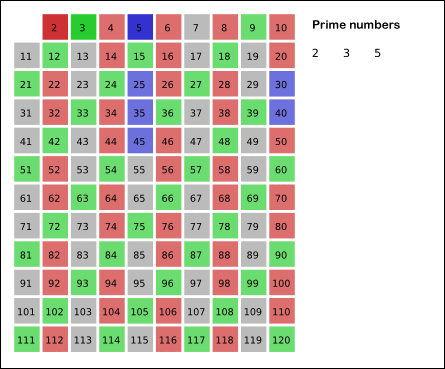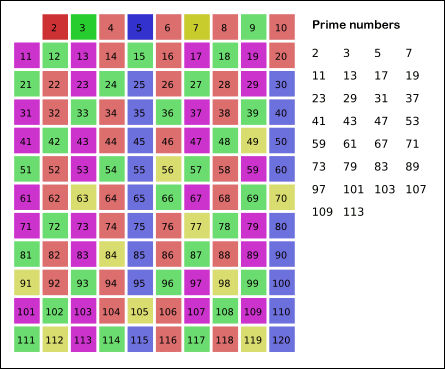
이미지 출처: https://ko.wikipedia.org/wiki/%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98_%EC%B2%B4
처음에 가장 작은 수인 2로 걸러내고, 또 3, 5, 7, … 이렇게 반복하고 걸러내는 동작은 11 이전의 소수인 7까지 진행합니다.
11의 제곱은 121로 120 보다 크기 때문입니다.
이에 대한 자세한 설명은 아래에 코드와 함께 설명하겠습니다.
for(i = 2 ; i*i <= N; i++){
if(Array[i] == true){
for(j = i*i ; j <= N ; j += i){
Array[j] = false;
}
}
}
첫 번째 for문에서 2~N까지 순회하는데, i*i가 N 이하일 때까지만 순환하는 이유는 무엇일까요?
- i는 이미 2~i-1 까지의 loop에 의해 걸러진 후이기 때문에 i의 배수 중에서 i*i 이상인 배수만 걸러내면 됩니다.
i가 현재 8이라고 할 때, 8x2, 8x3, … , 8x7 까지의 배수는 이미 걸러진 후이기 때문에 반복할 필요 없습니다.
- 따라서 i*i가 N이 넘으면 이미 다 채로 걸러진 것이기 때문에 종료하면 됩니다.
마무리
위의 코드를 통해 크기가 N인 배열에 소수 정보가 저장되었습니다.
이제 loop문을 통해 찾아낸 소수를 출력하기만 하면 됩니다.
전체 코드는 아래와 같습니다.
참고하세요.
public void findPrimeNumbers(int M, int N) {
if (N <= 1) {
return;
}
boolean[] Array = new boolean[N + 1];
for (int i = 2; i <= N; i++) {
Array[i] = true;
}
for (int i = 2; i * i <= N; i++) {
if (Array[i]) {
for (int j = i * i; j <= N; j += i) {
Array[j] = false;
}
}
}
for (int i = M; i <= N; i++) {
if (Array[i]) {
System.out.println(i);
}
}
}
중간에 채로 걸러내는 부분의 loop문 범위가 2부터인 이유는 M부터 시작하면 2~M까지 수의 배수가 완전히 걸러지지 않아 소수 외의 수가 남게 되기 때문입니다!
감사합니다.
Text by Chaelin. Photographs by Chaelin, Unsplash.